 |
| 第二個步驟就是把 24 個亂了的邊塊組合成 12 對同色的邊塊;完成此部份後就等於完降階的處理了。 |
| 組邊的原理其實就是,先從這24個邊塊中找到兩個顏色相同的,把他合併起來,由於合併後會把中心弄亂了,因此要找一個未合併的邊塊移到已合併邊塊的位置,然後再復完中心,這樣就完成組合一個邊塊了。不明白的可以看看下面詳細解說。 |
|
| |
|
| i) 第一至第十 Pair |
| 例子 |
 |
1. 首先先找其中一個顏色,假設我們先做白綠色的邊塊。 |
 |
2. 先把他移到這樣。 |
 |
3. 如果作 d 的移動,邊塊就會組合起來了,同時中心也就亂了,因此要找一個未組合的邊塊移到原來白綠邊塊的位置。 |
 |
4. 從頂/底層找到一個未組合的邊塊移下來,這邊可以用 R U' R' 把藍白/紅白的邊移下來到白綠邊塊原本的位置。 |
 |
5 .然後復原中心就成功組合一個邊塊了。 |
|
動畫示範 步驟 1 - 5 |
| |
6. 重覆上面的步驟直到剩下 2 個邊塊要組合。
有時頂/底層沒有亂掉的邊塊可以換下來的話,就在組合前亂掉的邊塊移上去就好了。 |
|
|
| |
| ii) 最後兩個 Pair |
 |
到了最後兩個 pair ,因為組合後就沒有亂了的邊塊可換下來,所以我們會用到一個簡單的公式把它們交換位置。
( 黑色的是指已組合的pair ) |
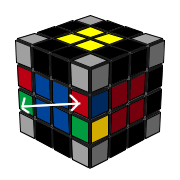 |
這個公式是 Dw R F' U R' F Dw' ,它的作用是如左圖把兩個邊塊交換。 |
|
來個動畫示範你就會明白! |
|
|
| 降階完後就是大家最愛的 3x3x3 了! |
| |
| << 回 Center |
|
往 Final Solve>> |
